Множественная регрессия. Регрессионные модели Регрессионный анализ в основах математического моделирования

В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных.

Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы - руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?

Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель - разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию - статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X . В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х 1 , Х 2 , …, X k ).

Скачать заметку в формате или , примеры в формате

Виды регрессионных моделей

где ρ 1 – коэффициент автокорреляции; если ρ 1 = 0 (нет автокорреляции), D ≈ 2; если ρ 1 ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ 1 = -1 (отрицательная автокорреляции), D ≈ 4.

На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями d L и d U для заданного числа наблюдений n , числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D < d L , гипотеза о независимости случайных отклонений отвергается (следовательно, присутствует положительная автокорреляция); если D > d U , гипотеза не отвергается (то есть автокорреляция отсутствует); если d L < D < d U , нет достаточных оснований для принятия решения. Когда расчётное значение D превышает 2, то с d L и d U сравнивается не сам коэффициент D , а выражение (4 – D ).

Для вычисления статистики Дурбина-Уотсона в Excel обратимся к нижней таблице на рис. 14 Вывод остатка . Числитель в выражении (10) вычисляется с помощью функции =СУММКВРАЗН(массив1;массив2), а знаменатель =СУММКВ(массив) (рис. 16).

Рис. 16. Формулы расчета статистики Дурбина-Уотсона

В нашем примере D = 0,883. Основной вопрос заключается в следующем - какое значение статистики Дурбина-Уотсона следует считать достаточно малым, чтобы сделать вывод о существовании положительной автокорреляции? Необходимо соотнести значение D с критическими значениями (d L и d U ), зависящими от числа наблюдений n и уровня значимости α (рис. 17).

Рис. 17. Критические значения статистики Дурбина-Уотсона (фрагмент таблицы)

Таким образом, в задаче об объеме продаж в магазине, доставляющем товары на дом, существуют одна независимая переменная (k = 1), 15 наблюдений (n = 15) и уровень значимости α = 0,05. Следовательно, d L = 1,08 и d U = 1,36. Поскольку D = 0,883 < d L = 1,08, между остатками существует положительная автокорреляция, метод наименьших квадратов применять нельзя.

Проверка гипотез о наклоне и коэффициенте корреляции

Выше регрессия применялась исключительно для прогнозирования. Для определения коэффициентов регрессии и предсказания значения переменной Y при заданной величине переменной X использовался метод наименьших квадратов. Кроме того, мы рассмотрели среднеквадратичную ошибку оценки и коэффициент смешанной корреляции. Если анализ остатков подтверждает, что условия применимости метода наименьших квадратов не нарушаются, и модель простой линейной регрессии является адекватной, на основе выборочных данных можно утверждать, что между переменными в генеральной совокупности существует линейная зависимость.

Применение t -критерия для наклона. Проверяя, равен ли наклон генеральной совокупности β 1 нулю, можно определить, существует ли статистически значимая зависимость между переменными X и Y . Если эта гипотеза отклоняется, можно утверждать, что между переменными X и Y существует линейная зависимость. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0: β 1 = 0 (нет линейной зависимости), Н1: β 1 ≠ 0 (есть линейная зависимость). По определению t -статистика равна разности между выборочным наклоном и гипотетическим значением наклона генеральной совокупности, деленной на среднеквадратичную ошибку оценки наклона:

(11) t = (b 1 – β 1 ) / S b 1

где b 1 – наклон прямой регрессии по выборочным данным, β1 – гипотетический наклон прямой генеральной совокупности, , а тестовая статистика t имеет t -распределение с n – 2 степенями свободы.

Проверим, существует ли статистически значимая зависимость между размером магазина и годовым объемом продаж при α = 0,05. t -критерий выводится наряду с другими параметрами при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к t-статистике – на рис. 18.

Рис. 18. Результаты применения t

Поскольку число магазинов n = 14 (см. рис.3), критическое значение t -статистики при уровне значимости α = 0,05 можно найти по формуле: t L =СТЬЮДЕНТ.ОБР(0,025;12) = –2,1788, где 0,025 – половина уровня значимости, а 12 = n – 2; t U =СТЬЮДЕНТ.ОБР(0,975;12) = +2,1788.

Поскольку t -статистика = 10,64 > t U = 2,1788 (рис. 19), нулевая гипотеза Н 0 отклоняется. С другой стороны, р -значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н 0 снова отклоняется. Тот факт, что р -значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.

Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы

Применение F -критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F -критерия. Напомним, что F -критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F -критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR , деленной на количество независимых переменных k ), к дисперсии ошибок (MSE = S Y X 2 ).

По определению F -статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR / MSE , где MSR = SSR / k , MSE = SSE /(n – k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F -распределение с k и n – k – 1 степенями свободы.

При заданном уровне значимости α решающее правило формулируется так: если F > F U , нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.

Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии

Аналогично t -критерию F -критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия ). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F -статистике – на рис. 21.

Рис. 21. Результаты применения F -критерия, полученные с помощью Пакета анализа Excel

F-статистика равна 113,23, а р -значение близко к нулю (ячейка Значимость F ). Если уровень значимости α равен 0,05, определить критическое значение F -распределения с одной и 12 степенями свободы можно по формуле F U =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > F U = 4,7472, причем р -значение близко к 0 < 0,05, нулевая гипотеза Н 0 отклоняется, т.е. размер магазина тесно связан с его годовым объемом продаж.

Рис. 22. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, с одной и 12 степенями свободы

Доверительный интервал, содержащий наклон β 1 . Для проверки гипотезы о существовании линейной зависимости между переменными можно построить доверительный интервал, содержащий наклон β 1 и убедиться, что гипотетическое значение β 1 = 0 принадлежит этому интервалу. Центром доверительного интервала, содержащего наклон β 1 , является выборочный наклон b 1 , а его границами - величины b 1 ± t n –2 S b 1

Как показано на рис. 18, b 1 = +1,670, n = 14, S b 1 = 0,157. t 12 =СТЬЮДЕНТ.ОБР(0,975;12) = 2,1788. Следовательно, b 1 ± t n –2 S b 1 = +1,670 ± 2,1788 * 0,157 = +1,670 ± 0,342, или + 1,328 ≤ β 1 ≤ +2,012. Таким образом, наклон генеральной совокупности с вероятностью 0,95 лежит в интервале от +1,328 до +2,012 (т.е. от 1 328 000 до 2 012 000 долл.). Поскольку эти величины больше нуля, между годовым объемом продаж и площадью магазина существует статистически значимая линейная зависимость. Если бы доверительный интервал содержал нуль, между переменными не было бы зависимости. Кроме того, доверительный интервал означает, что каждое увеличение площади магазина на 1 000 кв. футов приводит к увеличению среднего объема продаж на величину от 1 328 000 до 2 012 000 долларов.

Использование t -критерия для коэффициента корреляции. был введен коэффициент корреляции r , представляющий собой меру зависимости между двумя числовыми переменными. С его помощью можно установить, существует ли между двумя переменными статистически значимая связь. Обозначим коэффициент корреляции между генеральными совокупностями обеих переменных символом ρ. Нулевая и альтернативная гипотезы формулируются следующим образом: Н 0 : ρ = 0 (нет корреляции), Н 1 : ρ ≠ 0 (есть корреляция). Проверка существования корреляции:

где r = + , если b 1 > 0, r = – , если b 1 < 0. Тестовая статистика t имеет t -распределение с n – 2 степенями свободы.

В задаче о сети магазинов Sunflowers r 2 = 0,904, а b 1 - +1,670 (см. рис. 4). Поскольку b 1 > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t -статистику:

При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.

При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.

Оценка математического ожидания и предсказание индивидуальных значений

В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X .

Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов ) регрессионное уравнение позволило предсказать значение переменной Y X . В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X :

где , = b 0 + b 1 X i – предсказанное значение переменное Y при X = X i , S YX – среднеквадратичная ошибка, n – объем выборки, X i - заданное значение переменной X , µ Y | X = X i – математическое ожидание переменной Y при Х = Х i , SSX =

Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X i . Если значение переменной Y предсказывается для величин X , близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.

Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:

Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.

Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X , часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y X = Xi при конкретном значении переменной X i определяется по формуле:

Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:

Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.

Подводные камни и этические проблемы, связанные с применением регрессии

Трудности, связанные с регрессионным анализом:

• Игнорирование условий применимости метода наименьших квадратов.
• Ошибочная оценка условий применимости метода наименьших квадратов.
• Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
• Применение регрессионного анализа без глубоких знаний о предмете исследования.
• Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
• Путаница между статистической и причинно-следственной зависимостями.

Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?

Исследователь не должен увлекаться перемалыванием чисел - вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).

Рис. 23. Четыре набора искусственных данных

Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)

Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.

Рис. 25. Диаграммы разброса для четырех наборов данных

Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, - набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х 8 = 19, Y 8 = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.

Рис. 26. Графики остатков для четырех наборов данных

Как избежать подводных камней при регрессионном анализе:

• Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
• Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
• Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
• Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
• Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
• Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
• Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
• Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.

Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t -критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.

Рис. 27. Структурная схема заметки

Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872

Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.

Модель множественной регрессии

Дана модель множественной регрессии:

Номер предприятия	Номер предприятия

Постановка задачи

Требуется:

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.

3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

4. С помощью -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации.

5. С помощью частных -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после.

6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Процесс построения модели множественной регрессии

Найдем средние квадратические отклонения признаков:

1. Вычисление параметров линейного уравнения множественной регрессии.

Для нахождения параметров линейного уравнения множественной регрессии

необходимо воспользоваться готовыми формулами:

Рассчитаем сначала парные коэффициенты корреляции:

Таким образом, получили следующее уравнение множественной регрессии:

Коэффициенты и стандартизованного уравнения регрессии находятся по формулам:

Т.е. уравнение будет выглядеть следующим образом:

Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:

Вычисляем:

Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,627% или 0,170% соответственно.

Таким образом, подтверждается большее влияние на результат фактора, чем фактора.

2. Коэффициенты парной корреляции мы уже нашли:

Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы и явно коллинеарны, т.к.). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:

Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

Коэффициент множественной корреляции определить с помощью следующих формул:

Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом.

3. Нескорректированный коэффициент множественной детерминации оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 78,7% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации

определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 96%) детерминированность результата в модели факторами и.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи дает -критерий Фишера:

В нашем случае фактическое значение -критерия Фишера:

Получили, что (при), т.е. вероятность случайно получить такое значение -критерия не превышает допустимый уровень значимости. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи.

6. С помощью частных -критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после и фактора после при помощи формул:

Найдем и.

Получили, что. Следовательно, включение в модель фактора после того, как в модель включен фактор статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака оказывается незначительным, несущественным; фактор включать в уравнение после фактора не следует.

Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения после, то результат расчета частного -критерия для будет иным. , т.е. вероятность его случайного формирования меньше принятого стандарта. Следовательно, значение частного -критерия для дополнительно включенного фактора не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора является существенным. Фактор должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора.

Общий вывод состоит в том, что множественная модель с факторами и с содержит неинформативный фактор. Если исключить фактор, то можно ограничиться уравнением парной регрессии:

Регрессионный анализ – это наиболее известный метод построения модели идентификации. Он основан на двух предположениях:

1. метод применим только к математическим моделям линейным по идентифицируемым параметрам;
2. в качестве меры рассогласования математической модели с экспериментальными данными берется сумма квадратов отклонений расчетных и экспериментальных значений выходной величины.

Метод регрессионного анализа включает следующие этапы

1. Составление суммы квадратов отклонений расчетных и экспериментальных значений выходной величины (функция ошибки).
2. Минимизация функции ошибки. Для этого все частные производные функции ошибки по всем параметрам приравниваются к нулю.
3. Решение полученной системы линейных уравнений дает искомые значения параметров.

Идентификация линейной функции

Постановка задачи:

Решить задачу параметрической идентификации и найти параметры a 0 , a 1 , a 2 математической модели, имеющей следующую структуру: y = a 0 + a 1 x 1 + a 2 x 2 ; для наилучшего описания следующих экспериментальных данных.

Входные воздействия	x1	1	0	1	2
	x2	1	1	0	1
Выходное воздействие	y	-1	-3	3	1

Решение:

1. Составим сумму квадратов отклонений (функцию ошибки):

где N = 4 – количество экспериментов,
y iР – расчетное значение выходного воздействия,
y iЭ – экспериментальное значение выходного воздействия (из таблицы).
2. Минимизируем полученную функцию ошибки:

I(a 0 , a 1 , a 2) -> min

3. Применим необходимое условие существования экстремума (минимума) функции многих переменных.

Если непрерывная дифференцируемая функция имеет в некоторой точке экстремум, то ее градиент (вектор частных производных) равен нулю.

4. Вычислим частные производные функции ошибки и приравняем их к нулю:

5. Решим полученную систему линейных уравнений и находим три коэффициента "a".

Система решается достаточно просто, поэтому не будем расписывать её решение подробно. А ответ таков: a 0 = 1, a 1 = 2, a 0 = -4, то-есть полученная модель выглядит следующим образом: y = 1 + 2*x 1 - 4*x 2 .

С помощью метода наименьших квадратов.

Регрессионная модель объединяет широкий класс универсальных функций, которые описывают некоторую закономерность. При этом для построения модели в основном используются измеряемые данные, а не знание свойств исследуемой закономерности. Такая модель часто неинтерпретируема, но более точна. Это объясняется либо большим числом моделей-претендентов, которые используются для построения оптимальной модели, либо большой сложностью модели. Нахождение параметров регрессионной модели называется обучением модели .

Недостатки регрессионного анализа: модели, имеющие слишком малую сложность, могут оказаться неточными, а модели, имеющие избыточную сложность, могут оказаться переобученными .

В управлении и планировании существует целый ряд типовых задач, которые можно переложить на плечи компьютера. Пользователь таких программных средств может даже и не знать глубоко математику, стоящую за применяемым аппаратом. Он должен представлять лишь суть решаемой проблемы, готовить и вводить в компьютер исходные данные, интерпретировать полученные результаты. Программным продуктом, который можно использовать для этих целей, является Ms Excel .

Ms Excel - это не просто электронная таблица с данными и формулами для вычислений. Это универсальная система обработки данных, которая может использоваться для анализа и представления данных в наглядной форме.

Одной из чаще всего используемых возможностей Excel является экстраполяция данных - например, для анализа имеющихся фактических данных, оценки тенденции их изменения и получения на этой основе краткосрочного прогноза на будущее. В этом случае используется линейная экстраполяция данных на основе наименьшего квадратичного отклонения - отыскивается линейная зависимость данных, такая, которая бы минимизировала сумму квадратов разностей между имеющимися фактическими данными и соответствующими значениями на прямой линейного тренда (интерполяционной или экстраполяционной зависимости). На основе найденной зависимости можно сделать разумное предположение об ожидаемых будущих значениях изучаемого ряда данных.

Решение задач планирования и управления постоянно требует учета зависимостей одних факторов от других.

Рассмотрим различные методы представления зависимостей.

Если зависимость между величинами удаётся представить в математической форме, то имеем математическую модель.

Математическая модель - это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.

Математические модели могут быть представлены в виде формул, уравнений или систем уравнений. Например, зависимость времени падения тела на землю от первоначальной высоты описывается формулой . Рассмотрим примеры других способов представления зависимостей между величинами: табличного и графического . По результатам эксперимента мы составили таблицу и нарисовали график (рисунок 1).

Н (м)	t (сек)
	1,1 1,4 1,6 1,7 1,9 2,1 2,2 2,3 2,5

Рисунок1. Табличное и графическое представление данных.

Мы рассмотрели три способа отображения зависимости величин: функциональный (формула), табличный и графический. Но математической моделью процесса падения тела на землю можно назвать только формулу, т.к. формула универсальна. Таблица и диаграмма (график) констатируют факты, а математическая модель позволяет прогнозировать, предсказывать путем расчетов.

Статистические данные всегда являются приближенными, усредненными. Поэтому они носят оценочный характер. Однако, они верно отражают характер зависимости величин. И еще одно важное замечание: для достоверности результатов, полученных путем анализа статистических данных, этих данных должно быть много.

График искомой функции должен проходить близко к точкам диаграммы экспериментальных данных. Строить функцию так, чтобы ёе график точно проходил через все данные точки (рисунок 2), не имеет смысла. Во-первых, математический вид такой функции может оказаться слишком сложным. Во-вторых, уже говорилось о том, что экспериментальные значения являются приближенными.

Отсюда следуют основные требования к искомой функции:

Она должна быть достаточно простой для использования её в дальнейших вычислениях;

График этой функции должен проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика были минимальны и равномерны (рисунок 3).

Рисунок 3. Два варианта построения графической зависимости по экспериментальным данным.

Полученную функцию, график которой приведен на рисунке 3(б), принято называть в статистике регрессионной моделью. Регрессионная модель - это функция, описывающая зависимость между количественными характеристиками сложных систем.

Получение регрессионной модели происходит в два этапа:

1. Подбор вида функции;

2. Вычисление параметров функции.

Чаще всего выбор производится среди следующих функций:

y = ax + b - линейная функция;

y = ax 2 + bx + c - квадратичная функция;

y = aln(x) + b - логарифмическая функция;

y = ae bx - экспоненциальная функция;

y = ax b - степенная функция.

Если Вы выбрали (сознательно или наугад) одну из предлагаемых функций, то следующим шагом нужно подобрать параметры (a ,b, c и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точкам. Для этого подходит метод наименьших квадратов (МНК). Суть его заключается в следующем: искомая функция должна быть построена так, чтобы сумма квадратов отклонений у - координат всех экспериментальных точек от у - координат графика функции была бы минимальной.

Важно понимать следующее : методом наименьших квадратов по данному набору экспериментальных точек можно построить любую функцию. А вот будет ли она нас удовлетворять, это уже другой вопрос - вопрос критерия соответствия. На рисунке 4 изображены 3 функции, построенные методом наименьших квадратов.

Рисунок 4

Данные рисунки получены с помощью Ms Excel. График регрессионной модели называется трендом (trend - направление, тенденция).

График линейной функции - это прямая. Полученная по методу МНК прямая отражает факт роста заболеваемости от концентрации угарного газа, но по этому графику трудно что - либо сказать о характере этого роста. А вот квадратичный и экспоненциальный тренды - ведут себя очень правдоподобно.

На графиках присутствует ещё одна величина, полученная в результате построения трендов. Она обозначена как R 2 . В статистике эта величина называется коэффициентом детерминированности. Именно она определяет, насколько удачной получится регрессионная модель. Коэффициент детерминированности всегда заключен в диапазоне от 0 до 1. Если он равен 1, то функция точно проходит через табличные значения, если 0, то выбранный вид регрессионной модели неудачен. Чем R 2 ближе к 1, тем удачнее регрессионная модель.

Метод наименьших квадратов используется для вычисления параметров регрессионной модели. Этот метод содержится в математическом арсенале электронных таблиц.

Получив регрессионную математическую модель мы можем прогнозировать процесс путем вычислений. Теперь можно оценить уровень заболеваемости астмой не только для тех значений концентрации угарного газа, которые были получены путем измерений, но и для других значений. Это очень важно с практической точки зрения. Например, если в городе планируется построить завод, который будет выбрасывать в атмосфере угарный газ, то, рассчитав возможную концентрацию газа, можно предсказать, как это отразится на заболеваемости астмой жителей города.

Существуют два способа прогнозов по регрессионной модели. Если прогноз производится в пределах экспериментальных значений независимой переменной (в нашем случае это значение концентрации угарного газа - С), то это называется восстановлением значения .

Прогнозирование за пределами экспериментальных данных называется экстраполяцией.

Имея регрессионную модель, легко прогнозировать, производя расчеты с помощью электронной таблицы.

Табличный процессор дает возможность производить экстраполяцию графическим способом, продолжая тренд за пределы экспериментальных данных. Как это выглядит при использовании квадратичного тренда для С = 7 показано на рисунке 5.

Рисунок 5

В ряде случаев с экстраполяцией надо быть осторожным. Применимость всякой регрессионной модели ограничена, особенно за пределами экспериментальной области.

Список литературы.

1. Новиков Ф.А., Яценко А.Д.. Microsoft Office. С.-П.:БХВ-Петербург, 2002г. стр.449-458

2. Семакин И.Г., Хеннер Е.К. Информатика.11класс. М.: БИНОМ. Лаборатория знаний, 2003г. стр.102-117

Предметом регрессионного анализа является исследование зависимости случайной величины от совокупности случайных и неслучайных величин. Регрессионный анализ позволяет на основе выборочных наблюдений создать математическую модель зависимости результативного признака от факторных признаков.

В зависимости от количества факторных признаков модель регрессии может быть парной и многомерной. Запишем в общем виде зависимость результативного признака от совместного и одновременного влияния факторных признаков
(- количество факторных признаков)

(3.28)

где
- функция регрессии, которая выражает объективную закономерную зависимость результативного признака от совместного влияния факторных признаков;- случайная величина, выражающая влияние неконтролируемых и неучтенных факторов, а также ошибок измерения.

Из выражения (3.28) имеем

(3.29)

т.е. - отклонение результативного признака от среднего значения, вычисленного по функции регрессии.

Оценкой функции регрессии является уравнение регрессии

Для парной линейной регрессии выражение (3.28) имеет вид:

(3.31)

где
- параметры функции регрессии. Запишем уравнение регрессии для этого случая

(3.32)

где
- оценки параметров функции регрессии - параметры уравнения регрессии или просто параметры регрессии.

Методика получения уравнений парной линейной регрессии приведена в параграфах 3.7 и 3.10.

Парный нелинейный регрессионный анализ

Пусть по виду корреляционного поля точек предполагается нелинейная зависимость результативного признака от факторного признака. Запишем в общем виде уравнение парной нелинейной регрессии

(3.33)

Требуется определить параметры регрессии с помощью метода наименьших квадратов, математическая запись которого имеет вид:

и надстройки «Поиск решения».

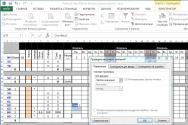
Размещение информации на рабочем месте ЭТ при определении параметров регрессии примера 3.5 с помощью надстройки “Поиск решения” представлено в таблице 3.15.

Таблица 3.15. Размещение информации

				Значение целевой функции

F2: = СУММКВРАЗН (e4:e18; d4:d18);

E4: = СУММПРОИЗВ(a4:c4;$a$2:$c$2);

H2: =КОРРЕЛ(d4:d18;e4:e18);I2: =СРЗНАЧ(d4:d18).

Результаты решения представлены в таблице 3.16.

Таблица 3.16. Результаты расчета

Анализ результатов расчета. В итоге расчета получено:

уравнение парной нелинейной регрессии

На рис.3.7 представлено уравнение парной нелинейной регрессии, полученное путем построения линии тренда. Анализ уравнений подтверждает их идентичность. Сравнение результатов расчета при парном линейном и нелинейном регрессионном анализе показывает, что они отличаются незначительно, т.е. для рассматриваемых признаков можно принять линейную модель регрессии.

Рис. 3.7. Уравнение линии тренда

Многомерный линейный регрессионный анализ

Обобщенная математическая модель многомерной линейной функции регрессии (3.28) имеет вид

где – количество факторных признаков;
– результативный признак;– отклонение;
– параметры функции регрессии.

Уравнение многомерной линейной регрессии для этого случая

Требование к факторным признакам, включаемым в математическую модель: факторы должны быть независимы друг от друга. Нарушение этого условия называется мультиколлинеарностью.

Коэффициенты уравнения регрессии получают с помощью инструмента «Регрессия» пакета анализа.

Анализ качества полученной модели проводится аналогично анализу парной линейной регрессии.